The Thales Theorem is also known as the basic proportionality theorem. The basic proportionality theorem was proposed by a Greek mathematician named Thales, that’s why it is also known as Thales Theorem.
The theorem is related to a special case of the inscribed angle theorem. The definition is also based on the diameter and angles of a circle.
What is Thales’ Theorem?
According to the Greek mathematician Thales, for any two equiangular triangles ( triangles having equal sides and equal angles are known as equiangular triangles), the ratio of any two corresponding sides is always the same.
The theorem of basic proportionality is based on this concept. It generally provides the relationship between two sides of an equiangular triangle.
The concept of the Thales Theorem is now introduced in similar triangles.
If two triangles are similar to each other then:-
- The corresponding angles of both triangles are equal
- The corresponding sides of both triangles are in proportion to each other
Statement of Thales or Basic Proportionality Theorem
The basic proportionality theorem which is also known as the Thales theorem, states that:
“If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are always in the same proportion”.
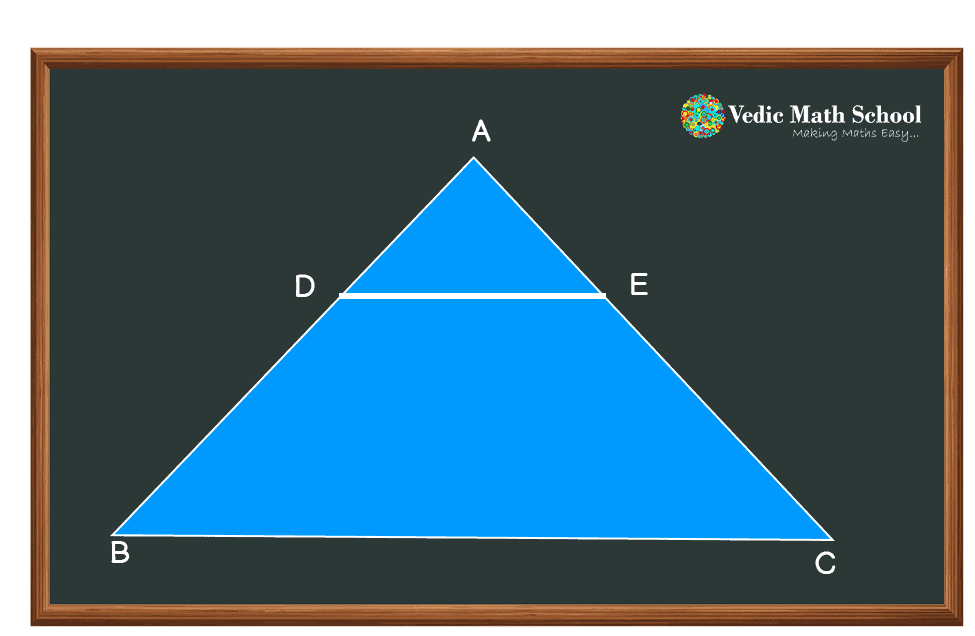
In the given figure, line DE is drawn parallel to side BC, so it joins the other two sides, AB and AC.
According to the basic proportionality or Thales theorem, it can be implied that:
D/DB = AE/EC
Read More: Decimals- Definition, Types, Properties, and Arithmetic Operations on Decimals
Proof of Thales Theorem
Now, let us try to prove our basic proportionality theorem of Thales theorem statement:-
Statement = “If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are always in the same proportion”.
Given: Let us consider a triangle ΔABC, as shown below. In this triangle, we draw a line DE parallel to the side BC of ΔABC and intersect the sides AB and AC at D and E, respectively.
Construction = In the above diagram join AB and CD, draw DP perpendicular to AC and EQ perpendicular to AB
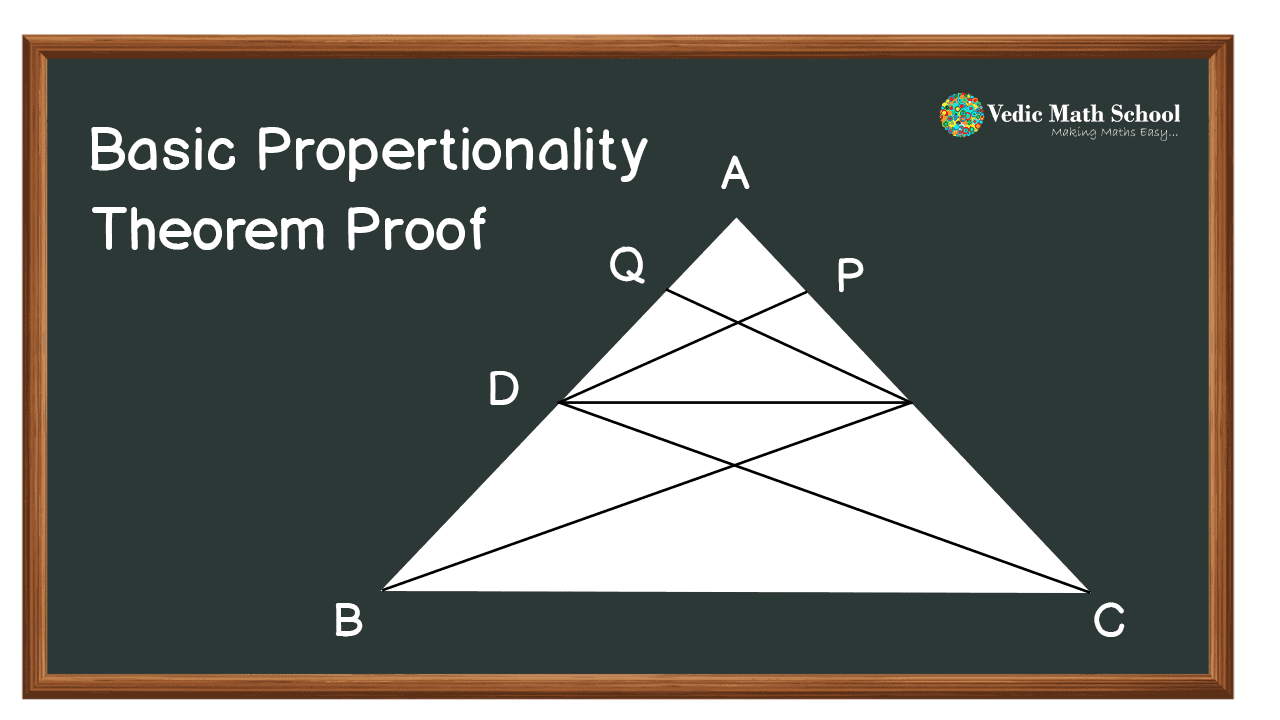
To Prove: AD/BD = AE/CE
Proof:-
Consider the triangles ADE and BDE. The base of both these triangles are the same which is AB and have equal height EQ.
Therefore,
(Area of ADE)/(Area of BDE) = (1/2 × AD × EQ)/(1/2 × BD × EQ) (Area of triangle = ½ * b * h )
(Area of ADE)/(Area of BDE) = AD/BD (equation 1 )
Now, let us consider triangles CDE and ADE. The base of both these triangles are also the same which is AC and have equal height DP.
So,
(Area of ADE)/(Area of CDE) = (1/2 × AE × DP)/(1/2 × CE × DP)
(Area of ADE)/(Area of CDE) = AE/CE (equation 2 )
Here, both triangles BDE and CDE are between the same set of parallel lines.
So, the Area of triangle BDE = Area of triangle CDE
Using equation 1 and 2 :-
AD/BD = AE/CE
Hence, Proved.
Read More : Let’s learn Plane and its Types
Corollary of Thales Theorem:
The basic proportionality theorem is also used to state the Mid Point theorem.
It states that a line segment which is drawn parallel to one side of a triangle and half of that side divides the other two sides at the midpoints.
Converse of Basic proportionality Theorem
According to the converse of the basic proportionality theorem “if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side”.
This is just the opposite of the Thales theorem, also known as the converse of the Thales Theorem.

Given:
PQR is a triangle and the line UV cuts the sides PQ and PR in equal proportion, so that = PU/QU = PV/RV
Proof=
Consider UV not parallel to QR and draw another line UX. But
given that: PU/QU = PV/RV
According to the above statements, we conclude=
PV/RV = PX/RX
Now, add 1 on both sides.
(PV/RV) + 1= (PX/RX) + 1
(PV + RV)/ RV = (PX + RX)/ RX
PV/RV = PX/RX
Therefore,
RV = RX
Hence the line UV is parallel to PR and it proves the converse of the basic proportionality theorem.
Read More : Compound Interest -Basics, Definition, Formula and solved examples
In Conclusion
Thales’ theorem is a fundamental theorem in geometry. This theorem has many applications in mathematics and engineering and is considered a cornerstone of Euclidean geometry.
Thales’ theorem is a testament to the brilliance of ancient mathematicians, who laid the foundations for modern mathematics through their groundbreaking work.
Today, Thales’ theorem continues to be an important concept in mathematics and serves as a foundation for many other mathematical theorems and concepts.