In geometry, a Triangle is a closed figure consisting of 3 angles, 3 sides and 3 vertices.
A triangle with three vertices A, B, and C is represented as △ABC. It is very common shape in geometry in which the 3 vertices are joined with each other. It is denoted by Symbol △.

In other words, we can define a triangle as a simple polygon with 3 sides from which two sides are joined end to end is called the vertex of the triangle and 3 interior angles. An angle is formed between two sides and each vertex forms an angle.

Table of Contents
Parts of a Triangle
A triangle mainly consists of three parts. They are: –
- 3 Angles
- 3 Sides
- 3 Vertices
Consider the given triangle PQR,it shows the vertices, sides and angles of the triangle: –

In the given triangle: –
- Angles are ∠PQR, ∠QRP, and ∠RPQ.
- Sides are side PQ, side QR, and side RP.
- Vertices are P, Q, and R.
Note: – The sum of all the angles of the triangle is equal to 180°.
Read More : Remember Multiplication Tables of Any Number Using Mental Mathematics
Properties Of Triangle
- A triangle has three sides, three angles, and three vertices.
- The sum of all the interior angles of a triangle is always 180 degrees. This property is known as the angle sum property.
- The sum of all exterior angles of a triangle is always 360 degrees.
- The sum of the lengths of any two sides of a triangle is greater than the length of the third side. This property is known as the triangle inequality theorem.
- The side which is opposite to the greater angle is the longest side.
- Similarly, the shortest side is always opposite the smallest interior angle.
- As the Pythagoras theorem states, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. (Hypotenuse² = Base² + Altitude²)
- The exterior angle of a triangle is always equal to the sum of the interior opposite angles. This property is known as the exterior angle theorem.
Read More : How to find HCF in 10 seconds
We can classify triangles on the basis of sides and angles.
Types Of Triangles On The Basis Of Sides
We can categorize triangles in 3 types on the basis of sides: –
- Equilateral Triangle
- Scalene Triangle
- Isosceles Triangle
Equilateral Triangle
As the name itself suggests, equilateral triangles have all three sides equal to each other. All three sides have the same length. In an equilateral triangle, the internal angles are of equal degrees, and each of the angles is 60°.
Read More : Find your LCM in 10 seconds
Scalene Triangle
The Scalene triangle is just the opposite of the equilateral triangle. It is a type of triangle, in which all three sides have different side measures. That’s why all three angles are also different from each other.

Isosceles Triangle
An isosceles triangle has two sides of equal length and two internal angles opposite to the two equal sides are also equal to each other.

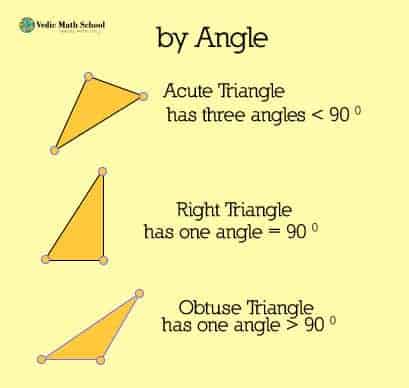
Types of Triangles On The Basis Of Angles
We can categorize triangles in 3 types on the basis of angles: –
- Acute Triangle
- Right Triangle
- Obtuse Triangle
Read More : Sum of cubes of n natural numbers
1. Acute Triangle
In an acute triangle, all the three angles measure less than 90°.
2. Right Triangle
When one of the angles of a triangle is 90°, it is known as the Right Triangle. It is also called the Right Angled Triangle.
3. Obtuse Triangle
When one of the angles of a triangle is obtuse that is more than 90°, it is known as the ObtuseTriangle. It is also called the Obtuse Angled Triangle.
Examples:
- If the length of all sides of a triangle is different from each other. Identify the type of triangle.
In a scalene triangle, the length of all the sides is different. Hence, this is a scalene triangle. - If the length of two sides of a triangle is equal. Identify the type of triangle.
In an isosceles triangle, the length of two sides is equal. Hence, this is an isosceles triangle. - If all the angles of a triangle are less than 90°. Identify the type of triangle.
In an acute triangle, all the angles are less than 90°. Hence, this is an acute triangle.
Read More : Fractions From Basics. Understand What is Fraction, Types with Examples
Triangle Formulae
In mathematics, for a two-dimensional figure ( 2 – D shape), there are only 2 basic measurements that we have to find out, which is the perimeter of the shape and area of the shape. A triangle is also a 2-dimensional figure, so we can find out its area and perimeter.
- The perimeter of the triangle
- Area of the triangle
1. The Perimeter of the Triangle
Perimeter of a triangle can be defined as the total measure or length of the outer boundary. In other words, we can say that, perimeter is the sum of all three sides of the triangle.
The word perimeter is made up of two Greek words – “peri” which means around and “metron” which means measure.
Read More : Subtraction of Fractions
” Perimeter = Sum of all the three Sides ”
The unit of the perimeter is the same as the unit of sides of the triangle.For eg: – if the length of the sides of the triangle is given in cm, the perimeter of the triangle will be also in cm.
If PQR is a triangle, where PQ, QR and RP are the lengths of sides, then the perimeter of triangle PQR is given by:
Perimeter = PQ+QR+RP

The perimeter of a triangle can be computed by the steps given steps below:
Step 1 = Firstly, note down the given measurements of all sides of a triangle.
Step 2 = Now, check that all the sides should have the same unit.
Step 3 = Simply add on the sides or calculate the sum of all the sides.
Step 4 = Write the final answer always along with the unit.
Now, Let us understand how we can find the perimeter of a triangle with the help of an example.
Read More : Polynomials From Basics! Types, Formula, Rules, Operation with Solved Examples
Example:
Find the perimeter of △PQR having the following dimensions: PQ= 7 cm, QR = 8 cm, PR = 9 cm.
Step 1= Check if all three sides of the triangle are given or not. Here,
PQ = 7 cm, QR = 8 cm, PR = 9 cm
Step 2 = Now, use the formula, Perimeter = PQ + QR + PR. Write the perimeter of the triangle along with its units.
Perimeter of triangle PQR = 7 + 8 + 9 = 24 cm.
2. Area Of The Triangle
Area of a triangle can be defined as the total region occupied by the three sides of a triangle in a 2-dimensional plane or the region enclosed within the sides of the triangle.
The area of a triangle can vary from one triangle to another depending on the length of the sides and the internal angles. The area of a triangle is always expressed in square units, for eg: – m2, cm2, in2, and so on.
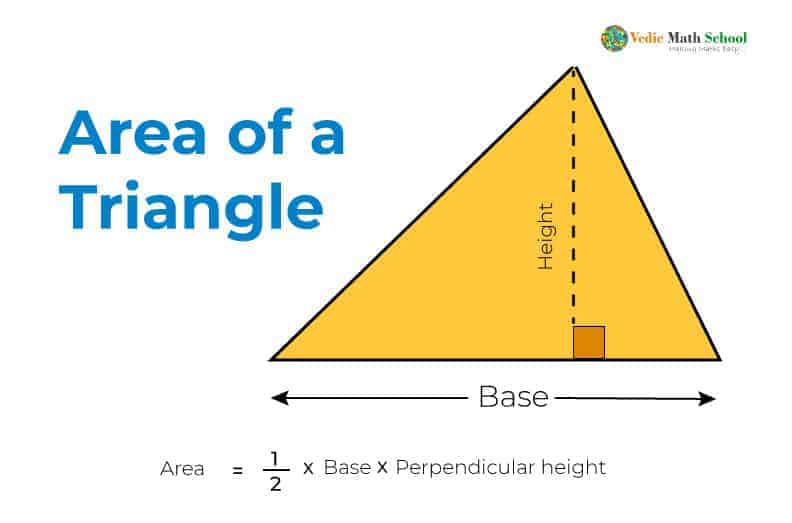
The basic formula used to calculate the area of a triangle is equal to half the product of its base and height.
A = 1/2 × b × h.
Read More : Interest – Do you know, what is Simple Interest?
This formula can be applied to all types of triangles. ( It can be a scalene triangle, an isosceles triangle, or an equilateral triangle).
As you all know, the base and the height of a triangle are perpendicular to each other.
The area of a triangle can be calculated using various formulas. For eg: – Heron’s formula or the trigonometric functions. However, we will discuss the basic formula that is applicable for all triangles, which is: –
Area of triangle = 1/2 × base × height
Consider the following diagram to see the base and height of a triangle: –
Now, Let us understand how we can find the area of a triangle using this formula with the help of an example.
Example: –
1. Find the area of a triangle with base ‘b’ = 3 m and height ‘h’ = 6 m?
Using the formula: –
Area of a Triangle: – A = 1/2 × b × h
= 1/2 × 3 × 6 = 9 m2
2. Find the area of a triangle with base ‘b’ = 13 cm and height ‘h’ =8 cm?
Using the formula: –
Area of a Triangle: – A = 1/2 × b × h
= 1/2 × 13 × 8 = 52 cm2







