The Uses and Versatility of Squares in Geometry

In mathematics, a Square is a 2-dimensional figure having four equal sides and equal angles. It is a plane figure. All the angles of a square are equal to 90°.

The square is very similar to the rectangle, the only difference between a square and a rectangle is that the rectangle has opposite sides equal in spite of having all equal sides.

The area and perimeter of the rectangle is also different from the square. In this article, we will learn about what is square?, its definition, properties, shape, area, and perimeter of the square, and some examples.

Table of Contents

Definition of Square:

A square can be defined as a regular quadrilateral, having all four sides of equal length and angles of equal measure. The diagonals of the square are also equal and bisect each other at 90°. All the angles of a square are aligned at right angles which means 90°.

It can also be defined as a rectangle having equal opposite sides.

Examples of square shapes are chessboards, square wall clocks,

The shape of a Square in Geometry

A square is a four-sided polygon with four right angles and four equal sides. In geometry, it is classified as a regular quadrilateral, which means that it has equal angles and sides. The shape of a square can be explained as:-

It is a four-sided polygon.
It has all sides of equal length.
It has all the angles of equal angle.
When we cut a square from the middle into two halves, both sides are symmetrical.

Properties of a Square in Geometry

A square is a special type of rectangle that has four equal sides and four right angles. There are various properties of the square. Some of them are given below:-

It is a closed two dimensional quadrilateral.
The interior angles of a square are equal to 90°.
A square has four vertices and four sides.
All the sides of the square have the same length or are equal. P
The opposite sides of a square are always parallel to each other.
The sides of a square are congruent with each other.
The diagonals of a square are also equal. They bisect each other at 90°.
The diagonal of the square divides it into two isosceles triangles.
In a square, the length of the diagonals is always larger than the length of the sides.
The sum of all interior angles of a square is 360°.

Formulae of a square

Now, we already know that square is a four-sided polygon with equal sides. There are generally three square formulas in geometry that are used to calculate area of the square, the perimeter of the square, diagonal of the square.

Let us understand each of the formula in detail:-

Now, we already know that square is a four-sided polygon with equal sides. There are generally three square formulas in geometry that are used to calculate area of the square, perimeter of the square, diagonal of the square.
Let us understand each of the formulas in detail:-

Perimeter of Square

The perimeter of a square can be defined as the total length of its boundary. It can be simply calculated by adding the length of all the sides. As a square has 4 sides, we must add the length of all the four sides to calculate its perimeter.

It can be written as:-

Perimeter of a Square in Geometry = side + side + side + side
So, perimeter = 4 * side

Let us understand it with a Few

Examples: The side of a square notebook is 30 cm, find its perimeter.

Answer = Side of the square notebook = 30 cm
perimeter of a square = (4 × Side)
= (4 × 30)
= 120 cm
So, the perimeter of the square notebook is 120 cm.

2. If the side of a square shape is 80 cm, find its perimeter.

Answer= Side of the square shape = 80 cm
perimeter of a square = (4 × Side)
= (4 × 80)
= 320 cm
So, the perimeter of the square shape is 120 cm.

Area of a square

The area of a square can be defined as the area or the space occupied by the figure. Area of a square can be calculated by the given formula:-
Area of a square = side * side = side2

Let us understand it with few

Examples: The side of a square chessboard is 8 inches, find the area of chessboard.

Answer =
Area of a square = side2
s2 = (8 × 8)
= 64 square inches.
So, the area of the square chessboard is 64 square inches.

The side of a square notebook is 12 inches, find the area of Notebook.

Answer:
Area of a square = side2
s2 = (12 * 12)
= 144 square inches.
So, the area of the notebook is 144 square inches.

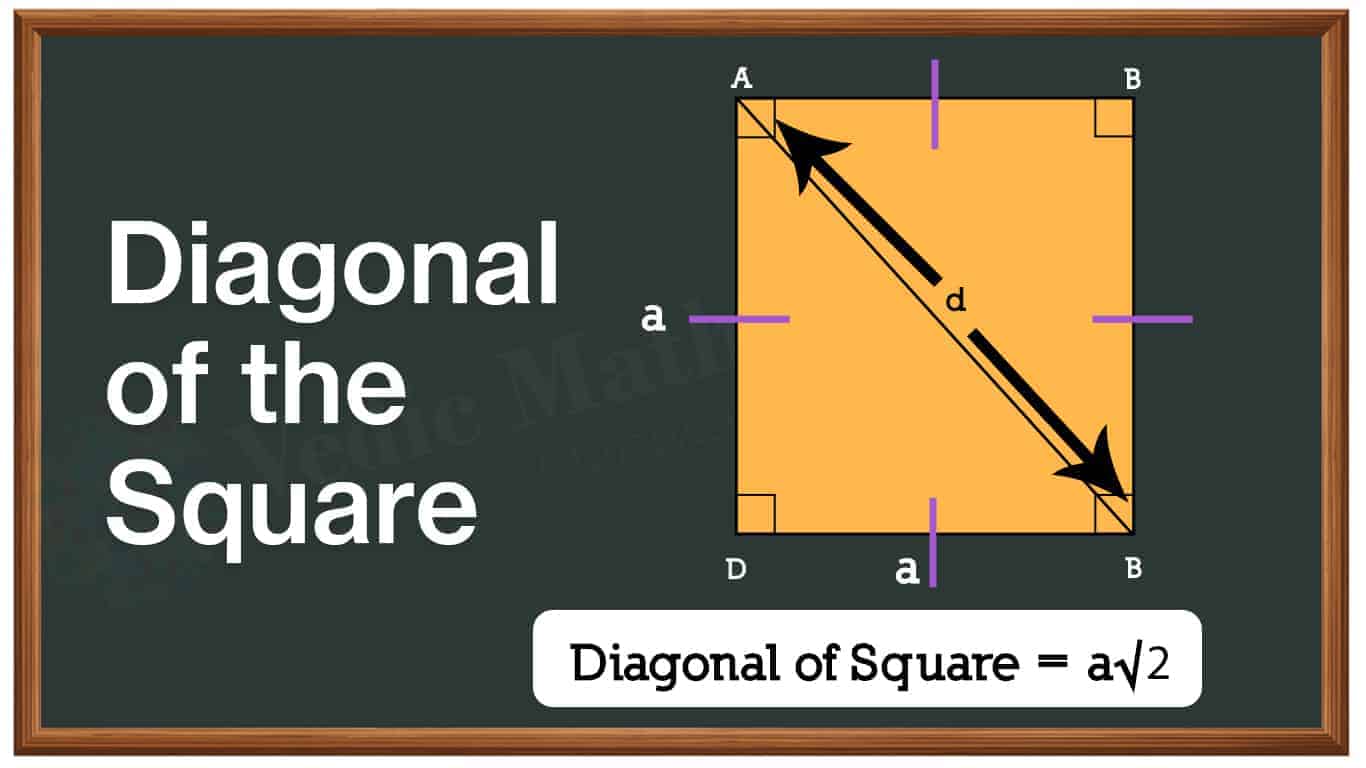
Diagonal of the Square

The diagonal of the square can be defined as a line segment that joins any of its two non adjacent vertices.
It can be calculated with the formulae :- side (√2)

Suppose if the side of a square is a, then its diagonal will be a√2.

Let us practice few Questions of this Formulae:-

Example 1. Find the diagonal of a square notebook whose side is 3 cm.

Solution:
Side of the square = 3 cm
Diagonal of a square (d) = a√2
Length of diagonal of square notebook = √2 × 3
= 4.23 cm ( √2 = 1.41 )

Example 2. Find the area of a square with a side length of 5 cm.

Solution:
A = s^2, where s is the length of one of the sides.
In this case,
s = 5 cm,
so A = 5^2 = 25 cm^2.
Therefore, the area of the square is 25 square centimeters.

Example 3.Find the length of the diagonal of a square with an area of 64 square meters.

Solution:
The area of a square can be found using the formula
A = s^2, where s is the length of one of the sides.
We are given that the area is 64 square meters, so we can solve for the length of one of the sides s, where
s = √A = √64 = 8 meters.

To find the length of the diagonal,
we can use the formula
d = s√2,
where d is the length of the diagonal and
s is the length of one of the sides.
Substituting in the value of s,
we get: d = 8√2 ≈ 11.31 meters.
Therefore, the length of the diagonal is approximately 11.31 meters.

Example 4. Find the perimeter of a square with an area of 36 square centimeters.

Solution:
As in the previous problem,
we can use the formula A = s^2 to solve for the
length of one of the sides: s = √A = √36 = 6 cm.

To find the perimeter, we can use the
formula P = 4s, where
P is the perimeter and
s is the length of one of the sides.
Substituting in the value of s,
we get: P = 4(6) = 24 cm.
Therefore, the perimeter of the square is 24 centimeters.

Example 5. Find the length of a side of a square whose diagonal is 10 centimeters.

Solution:
We can use the formula d = s√2
to solve for the length of one of the sides:
s = d/√2 = 10/√2 ≈ 7.07 cm.
Therefore, the length of one of the sides is approximately 7.07 centimeters.

FAQ’s ( Frequently asked questions)

1. What is the shape of a Square in Geometry?

Ans. It is a 4 sided polygon having equal sides and equal angles.

2. Square is a polygon or quadrilateral?

Ans. A square is a polygon and quadrilateral both.

3. How is a square different from a rectangle?

Ans. A square has all the sides of equal length while a rectangle has only opposite sides of equal length.

4. What are a few examples of squares in our daily life?

Ans. Chess board, square shaped ground, tiles and many more things.

5. What is the formula to find the area of a square?

A: The formula to find the area of a square is A = s^2, where “A” is the area and “s” is the length of one of the sides.

6. What is the formula to find the perimeter of a square?

A: The formula to find the perimeter of a square is P = 4s, where “P” is the perimeter and “s” is the length of one of the sides.

7. What is the measure of each angle in a square?

A: Each angle in square measures 90 degrees.

8. What is the length of the diagonal of a square?

A: The length of the diagonal of a square can be found using the formula d = s√2, where “d” is the length of the diagonal and “s” is the length of one of the sides.