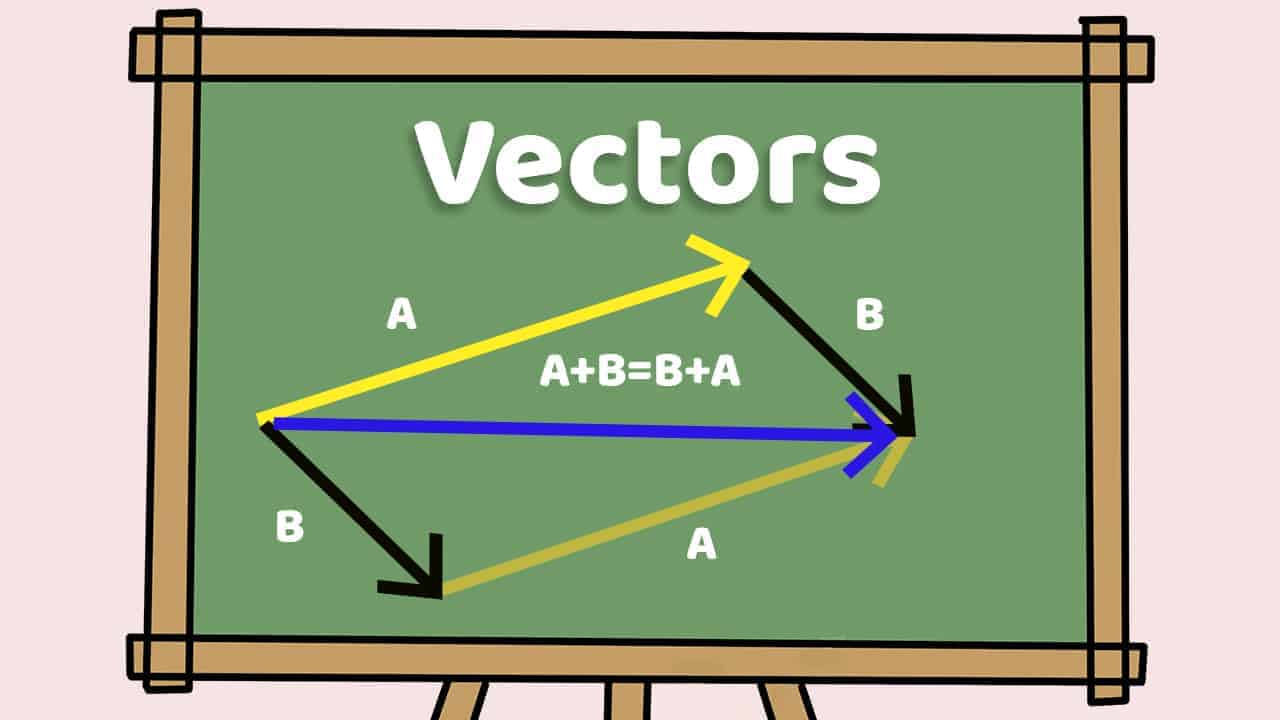
In mathematics, vectors are objects which have both magnitude and direction. The Magnitude defines the size of a vector. It is denoted or represented by a line with an arrow; they also have an initial point and a terminal point.
Vectors are also known as Euclidean vectors, geometric vectors, or simply a vector. Vectors are used to specify physical quantities such as displacement, velocity, acceleration, etc. Its concept is mainly used in physics.
In this article, we will learn the definition of vectors, types of vectors, formulas of vectors, and applications of vectors using a few solved examples.
Table of Contents
What are Vectors?
Vector is derived from a Latin word that means carrier. The vectors are defined as an object containing both magnitude and direction. They are used to describe the movement of an object from one point to another.
The initial point of a vector is also called the tail whereas the terminal point is called the head.
Vectors simply carry a point P to point Q.
The length of the line between the two points P and Q is referred to as the magnitude of the vector and the direction of the displacement of point P to point Q is referred to as the direction of the vector PQ.
Examples of Vectors
Vectors are used to calculate Velocity, Force, Acceleration, displacement etc as all of these quantities have directions and magnitudes or we can say these are the vector quantities.
Vector Notation or Representation of Vectors
As we already know, a vector has both magnitude and direction.
Vectors are generally denoted in bold lowercase letters such as a,v . We can also denote our vector using an arrow over the letter as →a.
For Example
vector AB can be denoted as –→AB.
Vector PQ can be denoted as —-> PQ.
The standard form of representation of a vector is:-
→P=x^i+y^j+z^k.
In this Example
, x,y,z are real numbers, and ^i,^j,^k are the unit vectors along the x-axis, y-axis, and z-axis respectively.
We will further discuss, what are unit vectors.

In the above image, the length of line AB is the magnitude and the head of the arrow points toward the direction.
Read More : Remember Multiplication Tables of Any Number Using Mental Mathematics
The Magnitude of a Vector and Magnitude of Formula
We can calculate the magnitude of the vector by taking the square root of the sum of the squares of its components.
The magnitude of a vector is represented by vertical lines on both sides of the given vector “|p|”. Magnitude represents the length of the vector.
If (a,b,c) are the components of a vector X, then the magnitude formula of X is given by,
|X| = √ (a2+b2+c2)
The magnitude of a vector is a scalar value.
Let us take an example to better understand the magnitude formula:-
Read More : METHODS FOR SOLVING QUADRATIC EQUATION
Example
Find the magnitude of vector x (6,4).
Solution-
In the given example,
Vector x = (6,4)
|x|= √(a2+b2)
|x|= √(62+42)
|x|= √(36+64) = √100
Therefore, | x |= 10
Types of Vectors
There are various types of vectors in mathematics. Some of them are:-
1. Unit Vector
2. Zero vector
3. Equal vector
4. Co-initial vectors
5. Negative vectors
6. Parallel vectors
7. Position vectors
8. Orthogonal vectors
1. Unit vectors
Unit vectors can be defined as vectors that have a magnitude equal to 1. It is denoted by a cap “^” or ^x. Unit vectors are also known as multiplicative identities of vectors.
The magnitude of a unit vector is always 1. It is generally used to denote the direction of a vector
Read More : Basic Concept Of Angles In Geometry
2. Zero Vector
A vector with zero magnitudes is called a zero vector. The coordinates of a zero vector are given by (0,0,0). The zero vector is denoted by a 0 with an arrow (→) at the top or simply 0.
The sum of any vector with zero vector or when we add any vector to zero vector, it is always equal to the vector itself. For example:- If “b” is any vector, the sum with zero vector will be:- 0+b = b
3. Equal Vectors
When the corresponding components of vectors are equal, then they are said to be equal. Equal vectors have the same magnitude and direction.
They can start and end from different initial and terminal points but the magnitude and direction should always be equal.
Read More : TRIANGLE: Definition, Parts, Properties,Types and Formulae
4. Co-initial Vectors
Vectors that share the same initial point are known as co-initial vectors.
5. Negative Vector
When two vectors have the same magnitudes but in opposite directions, they are known as negative vectors.
Suppose, If vectors P and Q have equal magnitude but directions are opposite, then vector P is known as the negative of vector Q or vice versa.
6. Parallel Vectors
When two or more vectors have the same direction but are not sure of the same magnitude (magnitude can be the same or cannot be the same) are known as parallel vectors.
Read More : Polynomials From Basics! Types, Formula, Rules, Operation with Solved Examples
7. Position Vectors
Position vectors are used to define the position and direction of the movement of vectors in a 3 D or three-dimensional space.
The magnitude and direction of the position vectors can be changed according to other entities. It is also known as the location vector.
8. Orthogonal Vectors
When the angle between two or more vectors is 90 degrees, they are said to be orthogonal vectors.
Read More : Interest – Do you know, what is Simple Interest?
Components of Vectors
Vectors can be divided into two main components in the two-dimensional space or x-y plane. They are:
- Horizontal Component
- Vertical Component
We break a vector into x and y components in the vector space to solve them.
Suppose, the vector “a” is inclined horizontally, having an angle equal to θ.
The vector “a” can be broken down into two components:- Ax and Ay.
Here, the component Ax is said to be a “Horizontal component” whose value is cos θ and component Ay is said to be a “Vertical component” whose value is sin θ.
Let us understand with an example:-
Read More: Circle- Basics, Definition, Formula, Parts, and Properties
Example:
A vector A, having a magnitude of 10 units & is inclined at 60°. Write a breakdown of the given vector into its two components.
Solution:
In the given example:- Vector A having magnitude|A| = 10 units and θ = 60°
Horizontal component (Ax) = A cos θ
Ax = 10 cos 60°
Ax = 10 × 0.5
Ax = 5 units
Now, Vertical component(Ay) = A sin θ
Ay = 10 sin 60°
Ay = 10 × √3/2
Ay = 10√3 units
Read More : Let’s learn Plane and its Types
Applications of Vectors
- Concepts of speed and velocity can be easily understood by Vectors.
- The direction of the force to move an object can also be determined using vectors.
- Vectors are used widely in engineering, mainly in civil engineering.
- In mathematics, it is used to study differential equations and differential geometry.
- Vectors are used in various oscillators.
- Vectors play a crucial role in quantum mechanics and fluid mechanics.
- It is also used in many wave propagations such as sound waves, AC waves, etc.
In the next article, we will discuss the operations performed on vectors, dot products, etc.
Practice Questions for you:
- What is the magnitude of vector b (0,4).
- Find the magnitude of vector a (24,70).
- A vector B, having a magnitude of 12 units & is inclined at 30°. Write a breakdown of the given vector into its two components.











