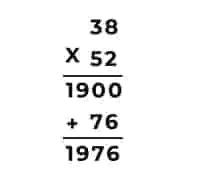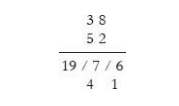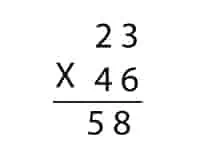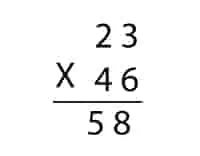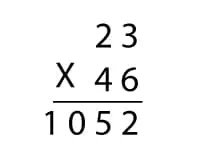Are you looking for a method that you can easily apply in your head for faster and more accurate solutions? If so, then you have come to the right place. Vedic Math has always helped us mentally solve complex problems using super easy, fun, and less time-consuming methods.
So today in this step-by-step tutorial we will explain how to solve the two-digit multiplication in a few seconds and save you time in the exam. Get ready to dominate your peers and impress your friends. Let’s go!
Traditional Approach to Do the Two-Digit Multiplication:
We all know how to multiply a Two-digit number by another Two-digit number. The multiplication starts with the one’s place first and then moves on to the tens place. The numbers are placed one below the other.
Then from the below Two-digit number, we multiply the number in the one’s place with the number that is above it. After that, from below the Two-digit number we multiply the number in ten’s place with the above number and write it below, with an extra zero rightwards.
We then add both the multiplied results to get the final result. Just like in an example below to help you recall.
As you can see, this method is too lengthy and it has many steps which increases the chances of making more mistakes.
Now let’s look at a method, which takes only a fraction of time compared to the previous method.
Video Tutorial: How to Do Two-Digit Multiplication Using Vedic Maths?
If you are a person like me who prefers video over text, we have a detailed step-by-step video tutorial for you where you can learn how to do Two-Digit Multiplication Using Vedic Maths. You can come along and watch the following video.
Video 1: Two-Digit Multiplication Video Tutorial
Video 2: Two-Digit Multiplication Video Tutorial
I also created these detailed step-by-step articles to explain the topic more easily. You will find this tutorial article worth reading. At the end of the article, I also included a Practice Questions Set that you can solve.
Two Digit Multiplication Using Vedic Maths: Urdhva Tiryagbhyam Method
The Urdhva-Tiryagbhyam Method is a very efficient and quick way to multiply two numbers, and it is especially useful when dealing with large numbers. This method also helps to improve mental math skills and enhances overall mathematical abilities. It is an important technique in Vedic Mathematics and is still used today by many worldwide.
Step-by-step explanation:
To get a better understanding, follow the video tutorial on this method. Anyway, here is the explanation in words, but after practising many problems, you can do everything in your mind for quick results.
Using Traditional Method of Multiplication:
Vedic Method of Multiplication:
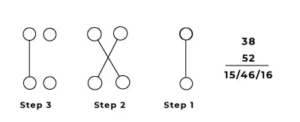
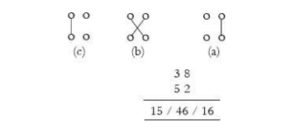
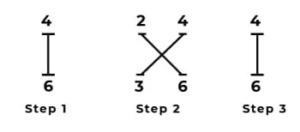
The Vedic Maths method consists of computing three steps as shown in the
picture below:
Steps:
- Step 1: Multiply the rightmost digits 8 and 2 to get 16.
- Step 2: Carry out a cross multiplication between 3 and 2, and 8 and 5 to get 6 and 40 respectively and on adding them, we get 46.
- Step 3: Multiply the leftmost digits 3 and 5 to get 15.
We have to retain one digit at each of the three locations and carry the surplus to the left. Hence in 15 / 46 / 16
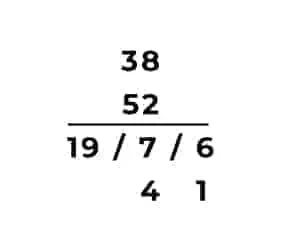
We start from the right, retain 6 and carry 1 to the left. This gives 47 in the middle location.
Now, we retain 7 and carry 4 to the left. We add 4 to 15 to get 19.
This gives 19 / 7 / 6 i.e. 1976 which is the required answer.
To speed up this operation, the carry digit can be written just below the number on the left. It can then be added to the number to its left at each operation itself.
Let’s see the multiplication again.
Here, the rightmost vertical multiplication is carried out first to get 8 × 2 = 16. We write 6 and write the carry 1 as shown.
Next, we carry out the cross multiplication 3 × 2 + 5 × 8 = 46, add the carry (1) to it, and get 47. We write down 7 and the carry digit 4 as shown.
The 3rd product is 3 × 5 which gives 15 to which we add the carry digit of 4 and get 19.
As you can see, the method gives you the final answer faster in just one line.
In other words:
For every two-digit number multiplication, we have to follow three steps.
Step 1: Multiply the digits in the first row vertically and write the result on the answer row. If the multiplication results in two digits, writing only the first digit in the answer second will be carried forward.
Step 2: For next digit multiplication, multiply numbers diagonally from the left top corner to the right bottom corner and add this value with a second diagonal line, i.e., right top right corner to the left bottom corner.
Step 3: This is the same as the first row, but we have to Multiply the last digits vertically and write the result on the answer row. Because this is the last number to multiply, we must write the complete number in the last.
After Step three, you have the result that is the product of the two numbers.
Understand with Examples:
Example: 1. Multiply 23 and 46 and write the Answer using the Urdhva-Tiryagbhyam Method.
Solution: Here, we have two digit numbers, 23 and 46, and we have to multiply each number one by one in the following pattern.
Step 1: Multiply the digits in the first row vertically and write the result on the answer row. If the multiplication results in two digits, writing only the first digit in the answer second will be carried forward.
Here 3 x 6 = 18. So we must write 8 in the answer row, and 1 will be carried forward.
Step 2: For next digit multiplication, multiply numbers diagonally from the left top corner to the right bottom corner and add this value with a second diagonal line, i.e., right top right corner to the left bottom corner.
So the number will be 2 x 6 + 4 x 3 = 24, and we have 1 carry from the last number, so it becomes 25. We write 5 in the answer row, and 2 will be carried forward.
Step 3: This is the same as the first row, but we have to Multiply the last digits vertically and write the result on the answer row. Because this is the last number to multiply, we must write the complete number in the last.
In this case, 2 x 4 = 8, and we have to add the last carry 2, so it becomes 10 and will write in the answer row.
So, the product of 23 and 46 is 1056.
Practice Problems for Two-Digit Multiplication
Here, we are going to let you solve some problems on your own. You must practice and grasp the concept well. After some practice problems, you will certainly be able to solve problems like these in your head, without even lifting your pen. Solve the Following Questions
- 43 X 21=?
- 32 X 45=?
- 23 X 46=?
- 32 X 21=?
- 32 X 45=?
- 43 X 21=?
- 53 X 47=?
- 4.7 X 5.3=?
You will find the video solutions to these questions in the below-mentioned video lecture on this topic. Make sure you watch the video till the end for faster calculations and accurate answers.
It’s Your Turn Now
Mastering two-digit multiplication using Vedic Maths not only saves time but also enhances your mental math skills significantly. By adopting the Urdhva-Tiryagbhyam method, you can solve complex problems in just a few steps, leaving behind the lengthy and error-prone traditional method.
With consistent practice, these techniques will soon become second nature, boosting your confidence and accuracy.
Don’t forget to practice the problems provided and check out the video tutorials for a visual guide.