Pythagorean Triple (Triples are known as triplets but triples is the majorly used term) can be defined as a set of 3 positive integers (integer is a whole number, it can be positive, negative or zero) a, b and c that fits in the pythagorean formula, which is : –
a2 + b2 = c2
In other words, we can say that Pythagorean Triple are any 3 positive integers that fit into the pythagorean theorem.
Pythagorean theorem states that , in any right angled triangle, the square of the hypotenuse is equal to the sum of the squares of base and height.
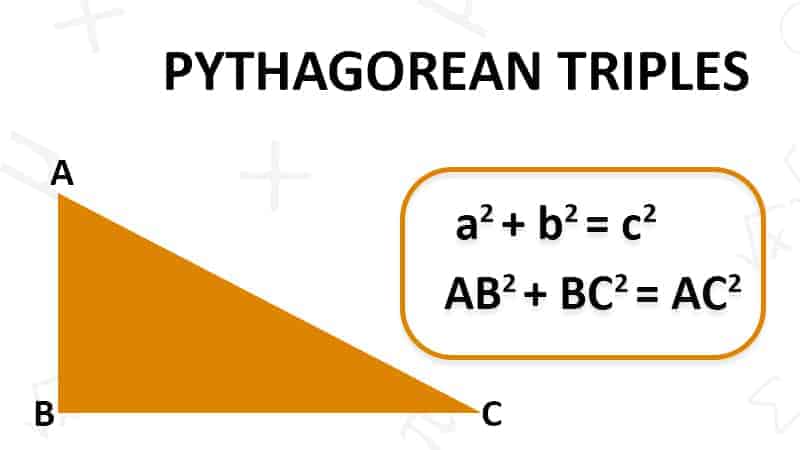
These 3 sides of a right angled triangle A, B and C form the pythagorean triples.
A2 + B2 = C2
Here A is altitude or height , B is our base and C is hypotenuse.
According to the figure: –
AB2 + BC2 = AC2
The smallest Pythagorean Triple exists is: – 3, 4 and 5
Let’s check this: –
Suppose a = 3, b = 4 and c = 5.
According to the formulae : –
a2 + b2 = c2
32 + 42 = 52
9 + 16 = 25
Some more examples to verify Pythagorean Triple : –
1. 5, 12 and 13
52 + 122 = 132
25 + 144 = 169
169 = 169
Hence , it is a pythagorean triplet.
2. 7, 24 and 25
72 + 242 = 252
49 + 576 = 625
625 = 625
Hence, it is a Pythagorean triplet.
Read More : Remember Multiplication Tables of Any Number Using Mental Mathematics
How Can We Generate Pythagorean Triples?
According to the figure, assume that: –
- a, and b are the legs of a right-angled triangle, a is the base and b is the height or altitude of the triangle.
- c is the hypotenuse of the right-angled triangle
- X and y are any two positive integers where x > y
- x and y are coprime numbers and both numbers should not be odd.
Now, we will use ‘x’ and ‘y’ to find the exact values of the sides.
- The length of side ‘a’ can be calculated by taking the difference between the squares of ‘x’ and ‘y’ which is expressed as
a = x2 – y2 - The length of side ‘b’ can be calculated by doubling the product of ‘x’ and ‘y’ which is expressed as : –
b = 2xy - At last, the length of side ‘c’ can be computed by the sum of the squares of x and y, which can be expressed as
c = x2 + y2
Read More : How to find HCF in 10 seconds
Now, three formulas are generated from our assumptions:
a = x2– y2
b = 2xy
c = x2+ y2
Note: – To generate some random Pythagorean triples, assume random natural numbers x and y, such that x > y and compute the triples (a,b,c) such that
a = x2– y2, b = 2xy, c = x2+ y2
Let us generate Pythagorean triples to better understand the steps: –
Given two integers are 2 and 3, generate a Pythagorean Triple from them?
Assume x = 3, y = 2
Hence x > y, x = 3, and y = 2.
Read More : METHODS FOR SOLVING QUADRATIC EQUATION
Now, simply put the values into the formulas of a, b, and c, to get the sides of the right triangle.
Computing a:
a = x2 – y2
a = 32 – 22
9 – 4 = 5
a = 5
Computing b:
b = 2xy
b = 2 × 3 × 2
b = 12
Computing c:
c = x2 + y2
c = 32 + 22
c = 13
Let us check if our values for a = 5, b = 12, and c = 13 satisfy the Pythagorean theorem, which is a2 + b2 = c2 LHS:
52 + 122 = 25 +144 = 169
RHS : 132 = 169
Therefore, (5, 12, 13) are Pythagorean triples.